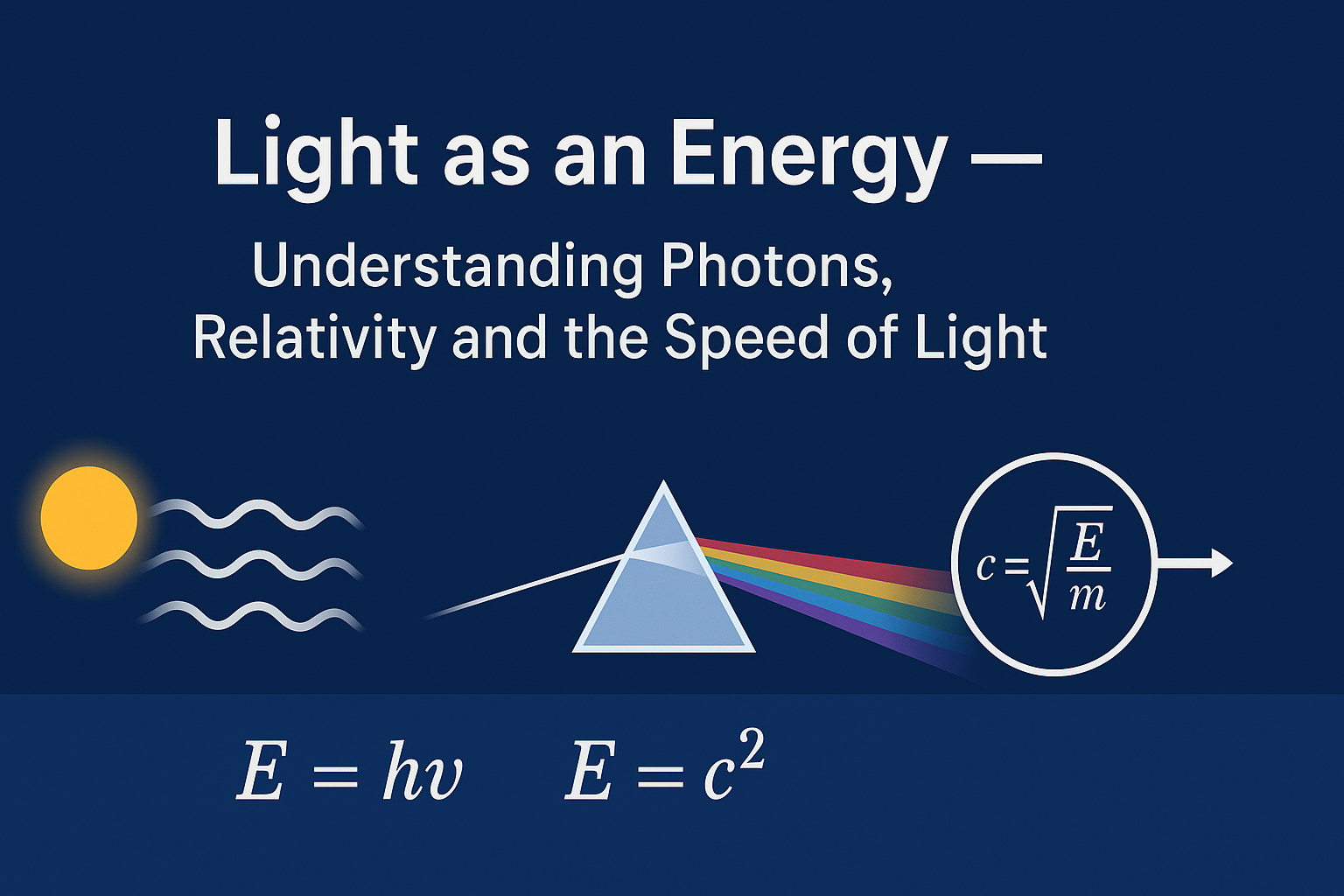
A descriptive explanation of light, photon energy, mass–energy equivalence, the role of the speed of light, and how time behaves in the presence of light.
1. What is Light?
Light is electromagnetic radiation that behaves as both a wave and a particle. As a wave, it has frequency \( \nu \) and wavelength \( \lambda \). As a particle, it is made of packets of energy called photons.
2. Electromagnetic Spectrum
Light spans radio waves, microwaves, infrared, visible light, ultraviolet, X-rays and gamma rays. All follow: \[ c = \lambda \nu \]
3. Photon Energy — \( E = h\nu \)
A single photon's energy is described by:
Since \( \nu = \frac{c}{\lambda} \), photon energy can also be written as:
4. Mass–Energy Equivalence — \( E = mc^2 \)
Einstein showed that mass and energy are two forms of the same entity:
This equation gives the rest energy of matter. Even if an object is not moving, its mass contains energy.
5. A deeper relationship — Energy, Momentum and Mass
The general form that applies to all particles is:
For photons, \( m = 0 \), so: \[ E = pc \quad \text{and} \quad p = \frac{h}{\lambda} \]
6. Showing Relation: \( c = \sqrt{E/m} \)
From Einstein's equation \( E = mc^2 \), we can isolate the speed of light:
This form shows that the speed of light works like a square–root conversion factor between mass and energy. But remember: this applies only to rest mass energy, not photon energy.
7. More Light-Speed Relations
Wave relation:
Photon momentum relation:
Photon energy in terms of wavelength:
Relativistic energy form:
These equations connect light, energy, frequency, wavelength and motion.
8. Light and Time — How Time Behaves with Light
Light plays a fundamental role in the nature of time. According to relativity:
- The speed of light \( c \) is the same for all observers.
- Time slows down as an object's speed approaches \( c \).
- A photon experiences no passage of time — from emission to absorption.
This leads to **time dilation**, described by:
As \( v \to c \), the denominator approaches zero, making \( t' \) extremely large. This means time slows down dramatically at near-light speeds.
Light therefore defines how we measure distance, time, and causality in the universe — it is the maximum speed at which information and energy can travel.
9. Applications of Light–Energy Relations
- Solar energy and photovoltaics
- Lasers and optical communication
- Nuclear energy (mass-to-energy conversion)
- Medical imaging: X-ray, PET, radiation therapy
- Astronomy: measuring star temperature and distance
10. Summary
- Photon energy: \( E = h\nu \)
- Mass–energy relation: \( E = mc^2 \)
- General energy: \( E^2 = (pc)^2 + (mc^2)^2 \)
- Speed of light relations: \( c = \lambda\nu \), \( c = \sqrt{E/m} \)
- Light influences the nature of time and spacetime